Zeno of Elea is a Greek logician and philosopher who is mainly known for the paradoxes named in his honor. Not much is known about his life. The hometown of Zeno is Elea. Also in the writings of Plato, the meeting of the philosopher with Socrates was mentioned.
Around 465 BC e. Zeno wrote a book in which he outlined all his ideas. But, unfortunately, it has not reached our days. According to legend, the philosopher died in a battle with a tyrant (presumably the head of Elea Nearch). All information about Elea was collected bit by bit: from the works of Plato (born 60 years later Zeno), Aristotle and Diogenes Laertius, who wrote three centuries later a book of biographies of Greek philosophers. Zeno is also mentioned in the writings of the later representatives of the school of Greek philosophy: Themisty (4th century A.D.), Alexander Afrodinsky (3rd century A.D.), as well as Philoponus and Simplicius (both lived in the 6th century A.D.). Moreover, the data in these sources are so well consistent with each other that all the ideas of the philosopher can be reconstructed from them. In this article we will tell you about the paradoxes of Zeno. So let's get started.

Paradoxes of the set
Ever since the era of Pythagoras, space and time were considered exclusively from the point of view of mathematics. That is, they were believed to be composed of many points and points. However, they have a property that is easier to sense than to define, namely “continuity”. Some Zeno paradoxes prove that it cannot be divided into moments or points. The philosopher’s reasoning boils down to the following: “Suppose that we have completed the division to the end. Then only one of the two options is true: either we get the minimum possible quantities or parts that are indivisible, but infinite in quantity, or division will lead us to parts without magnitude, since continuity, being homogeneous, must be divisible under any circumstances. It cannot be divisible in one part, but not in the other. Unfortunately, both results are pretty ridiculous. The first is due to the fact that the division process cannot end while there are parts in the remainder that have a value. And the second one is because in such a situation, initially the whole would have been formed from nothing. ” Simplicius attributed this argument to Parmenides, but it is more likely that its author is Zeno. We go further.
Zeno's Paradoxes of Motion
They are considered in most books devoted to the philosopher, because they come into dissonance with evidence of the feelings of the Eleatics. In relation to the movement, the following Zeno paradoxes are distinguished: “Arrow”, “Dichotomy”, “Achilles” and “Stages”. And they came to us thanks to Aristotle. Let's take a closer look at them.
"Arrow"
Another name is the Zeno quantum paradox. The philosopher claims that any thing either stands still or moves. But nothing is in motion if the occupied space is equal to it in length. At a certain moment, the moving arrow is in one place. Therefore, it does not move. Simplicius formulated this paradox in short form: “A flying object occupies an equal place in space, but that which takes an equal place in space does not move. Therefore, the arrow is at rest. ” Femistius and Phelopon formulated similar options.
"Dichotomy"
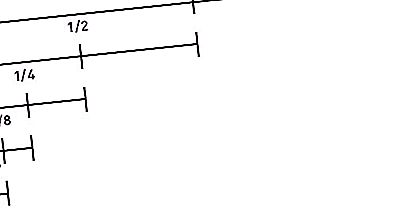
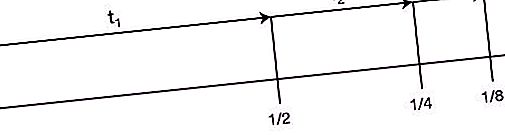
Takes second place in the list of "Zeno Paradoxes". It reads as follows: “Before an object that begins to move can travel a certain distance, it must overcome half of this path, then half of the remaining, etc. to infinity. Since during repeated divisions of the distance in half, the segment becomes finite all the time, and the number of these segments is infinite, this distance cannot be overcome in a finite time. Moreover, this argument is true both for small distances and high speeds. Therefore, any movement is impossible. That is, the runner will not even be able to start."
This paradox commented in great detail on Simplicius, indicating that in this case an infinite number of touches must be made in a finite time. “Anyone who touches anything can count, but the infinite set cannot be sorted out or counted.” Or, as Philopon put it, an infinite set is indefinable.
Achilles
Also known as the paradox of the Zeno tortoise. This is the most popular philosophical argument. In this paradox of movement, Achilles competes in a run with a turtle, which is given a small handicap at the start. The paradox is that the Greek warrior will not be able to catch up with the turtle, since first he will reach the place of its start, and she will already be at the next point. That is, the turtle will always be ahead of Achilles.
This paradox is very similar to a dichotomy, but here the infinite division goes according to progression. In the case of a dichotomy, there was a regression. For example, the same runner cannot start, because he cannot leave his location. And in the situation with Achilles, even if the runner starts moving, he still will not come running anywhere.
"Stage"
If we compare all the paradoxes of Zeno in terms of complexity, then this would be the winner. It is more difficult than others to expound. Simplicius and Aristotle described this reasoning fragmentarily, and one cannot rely on its reliability with 100% certainty. The reconstruction of this paradox has the following form: let A1, A2, A3 and A4 are motionless bodies of equal size, and B1, B2, B3 and B4 are bodies of the same size as A. B bodies move to the right so that each B passes And in one instant, which is the smallest period of time of all possible. Let B1, B2, B3 and B4 be bodies identical to A and B, and move relative to A to the left, overcoming each of the bodies in one instant.
Obviously, B1 overcame all four bodies of B. Let us take for a unit the time it took for one body of B to go through one body of B. In this case, four units were needed for all movement. However, it was believed that the two moments that passed for this movement were minimal and therefore indivisible. It follows that four indivisible units are equal to two indivisible units.